Школа по плазмохимии для молодых ученых России и стран СНГ
[ О Школе|Лекции|Секция 1|Секция 2|Секция 3|Секция 4|Секция 5|Cодержание |
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ ПОЛОЖИТЕЛЬНЫХ ИОНОВ В ДВОЙНОМ ЭЛЕКТРИЧЕСКОМ СЛОЕ ЗОНДА
Е.В. Соколов
Ивановский государственный университет
В данной работе выведено аналитическое выражение для функции распределения ионов, попадающих на коллектор двухэлектродного зонда, учитывающее изменение углового распределение ионов в исходном потоке в области задерживающего потенциала и наличие столкновений в слое объемного заряда.
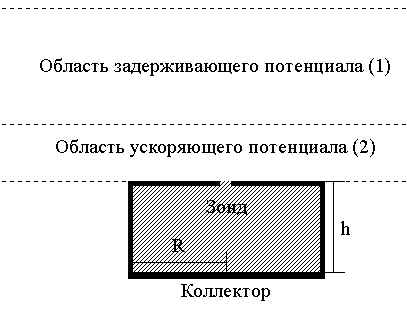
Рис. 1
Расчетная формула выводилась при следующих основных допущениях:
(l >
si, i=1,2
означает отсутствие
столкновений) и функции
распределения по углам после
столкновения F i(r, j ), 0 
r 
si, i=1, 2, 0 < j
< p
(все углы
отсчитываются от оси системы,
положительным считается
направление к зонду, F 1(0, j ) –
распределение по углам в
исходном потоке), максимальное
число столкновений n1 и n2.Для потока ионов, имеющих скорость V0 при проникновении в систему, и для каждого значения задерживающего потенциала U3=U3(h)-U3(0) требуется определить функцию F (V0, U3) – долю ионов, попавших на коллектор.
В силу упругости
столкновений и предположения о том,
что движение ионов происходит без
испускания энергии, скорость иона в
любой точке зависит лишь от
начальной скорости V0 и расстояния до
верхней границы области 1. Будем
считать, что 
e.(U1(s1)–U1(0)) и 
e.(U1(s1)–U1(0))
+ e.(U2(s2)–U2(0))
+ e.Uзад
(это условие является необходимым
для попадания на коллектор).
Пусть плоскости s 1 и s 2 лежат в области i (i=1, 2) и пусть расстояния от этих плоскостей до верхней границы области i равны r1 и r2, соответственно, причем r2 > r1. Предположим, что столкновения происходят только в плоскости s 1. Определим вероятность того, что ион, испытавший столкновение в плоскости s 1, достигнет плоскости s 2.
Для области 1.
В силу
монотонности функции U1(r) и отсутствия
столкновений выше плоскости s 2, после столкновения
для иона имеется две возможности:
либо пересечь верхнюю границу и
навсегда покинуть систему, либо
достичь плоскости s 2. Очевидно к первой
группе относятся все ионы, для
которых 
< |
j | p
(j –
угол после столкновения). Среди
остальных достичь плоскости s 2 могут лишь те,
вертикальная составляющая
кинетической энергии которых
удовлетворяет условию:
cos2j = (
– e(U1(r1)–U1(0)))
cos2j e (U1(r2)–U1(r1)),
откуда | j | arccos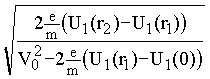
=j
1(V0, r1, r2) (вследствие
ограничения на V0 подкоренное выражение
всегда неотрицательно и меньше
единицы).
Для области 2.
Если ион
пересечет верхнюю границу области
2, он будет дополнительно ускорен
полем в области 1 и потому также
покинет систему; поэтому для
области 2 существуют те же две
возможности. В данном случае
плоскости s 2 достигнут все ионы с | j | 
, а
также те, для которых:
cos2j = (
– e(U1(s1)–U1(0))–e(U2(r1)–U2(0)))
cos2j e (U2(0)–U2(r1)) и
< | j | p
,
откуда | j | p
–arccos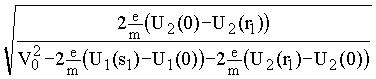
=j 2(V0, r1, r2) (выражение определено
по тем же причинам, что и в первом
случае).
Таким образом, искомая вероятность определяется следующим образом:
,
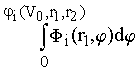i=1, 2.
Пусть Gi(V0, k, l 1, ... , l
k), k=1,2,..., l j>0,
l 1+...
+l k si – вероятность того,
что ион, испытав в точности k-1
столкновений, достиг плоскости r ,
находящейся на расстоянии r = l 1+... +l k от верхней границы
области i (i=1, 2), причем длины
свободного пробега равны,
соответственно, l 1, ... , l k.
Из предыдущей формулы следует, что:
Gi(V0, k, l 1, ... , l
k) =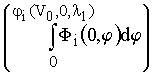
... 
.
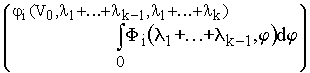Пусть плоскость r
лежит в области i (i=1, 2) на расстоянии r от верхней границы, и
пусть столкновения происходят лишь
в плоскости r . Определим функцию Hi(r, y ), 0 y <
, – распределение по
углам на нижней границы области r .
Для области 1.
Очевидно, должно выполняться следующее условие:
(
–
e (U1(r)–U1(0))) cos2j –e (U1(s1)–U1(r))
= (
– e (U1(s1)–U1(0)))
cos2y ,
где j – угол после столкновения,
откуда j =
arccos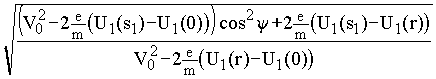
= y 1(V0, r, y ) (при
сделанных предположениях
выражение определено).
Очевидно H1(V0, r, y ) =F 1(r, y 1(V0, r, y )).
Для области 2.
Аналогично:
(–
e (U1(s1)–U1(0)) – e (U2(r)–U2(0)))
cos2j –
e (U2(s2)–U2(r)) =
= (
– e (U1(s1)–U1(0))
– e (U2(s2)–U2(0))) cos2y .
Так как при r < s2 правая часть уравнения положительна, решения существуют лишь при условии, что
| y | arccos
=
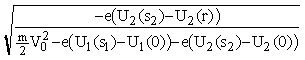(V0):
j' = arccos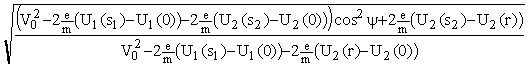
=
(V0, r, y ),
j''= p –arccos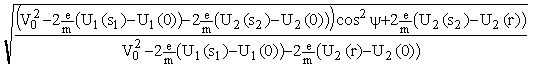
=
(V0, r, y ).
Тогда: H2(V0, r, y ) =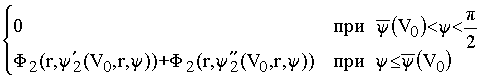
.
Легко видеть, что функция распределения по углам на нижней границе области i (i=1, 2) ионов, испытавших в точности k столкновений, k=0, 1, 2,... , имеет следующий вид:
Fi(V0, k, y ) =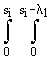
... 
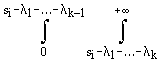L i(l 1)... L i(l k+1)Fi(V0, k, l 1, ... , l k)Hi(V0, l 1+... +l k, y )dl 1...dl k+1.
Таким образом,
функция Y 1(V0, y ) =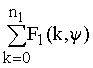
, 0 y < 
, представляет собой
функцию распределения по углам на
нижней границе области 1. Полагая F 2(0, j ) = Y 1(V0, y ),
получим функцию Y 2(V0, y ) =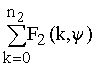
– функцию
распределения по углам на нижней
границе области 2.
Несложные вычисления позволяют определить функцию q (V0, U3) – максимальный угол наклона траектории иона на нижней границе области 2, при котором возможно попадание на коллектор:
q (V0, U3) =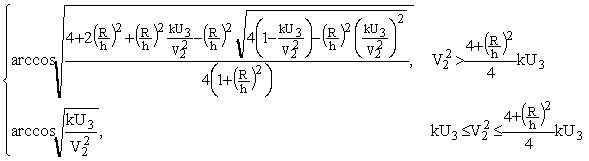
где k = 2
, 
=
– 2
(U1(s1)–U1(0))
– 2(U2(s2)–U2(0)).
Таким образом, получаем функцию распределения по V0 и U3 на коллекторе:
F (V0, U3) =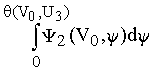
.
Умножив данную функцию на распределение по скоростям в исходном потоке F 0(V0) и пронормировав полученное выражение по V0, будем иметь функцию распределения J (U3), регистрируемую коллектором зонда.
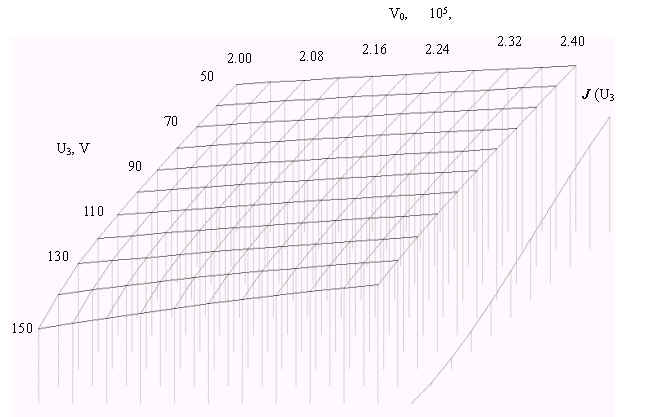
В настоящее время написана программа вычисления функции F (V0, U3) в заданном диапазоне параметров с заданной точностью (пример расчета приведен в таблице 1, а его графическое представление – на рисунке 2). В дальнейшем планируется разработка программы для вычисления функции распределения по скоростям в исходном потоке F 0(V0) по функциям J (U3) и F (V0, U3) с использованием метода регуляризации Тихонова.
Таблица 1.
Результат расчета функции F (V0, U3) для следующих параметров:
20000 V0 24000,
количество точек – 11, 50 U3 150,
количество точек – 11, число
отрезков разбиения при численном
интегрировании – 7.
[ О Школе|Лекции|Секция 1|Секция 2|Секция 3|Секция 4|Секция 5|Cодержание |