
Школа по плазмохимии для молодых ученых России и стран СНГ
[ О Школе|Лекции|Секция 1|Секция 2|Секция 3|Секция 4|Секция 5|Cодержание |
МОДЕЛИРОВАНИЕ НИЗКОТЕМПЕРАТУРНОЙ ПЛАЗМЫ ГАЗОВОГО РАЗРЯДА ПОНИЖЕННОГО ДАВЛЕНИЯ
В.В.Рыбкин
Ивановский государственный химико-технологический университет
I . ЦЕЛИ И ЗАДАЧИ МОДЕЛИРОВАНИЯ
Конечной целью любого моделирования является количественное описание свойств системы на основе параметров, определяющих ее состояние. Выбранные для описания свойства системы и описывающие их уравнения составляют содержание модели. Количество необходимых для решения этих уравнений параметров, которые считаются известными, определяет степень априорности модели, ее предсказательную способность. Чем меньше таких параметров, тем глубже модель описывает взаимосвязи, имеющие место в системе, тем модель сложнее. Исключение тех или иных параметров из набора заданных требует расширения содержания модели, т.е. введения новых уравнений, решением которых являются эти параметры. Таким образом, каждая более сложная модель включает в себя более простые подмодели предыдушего уровня.
Внешними, задаваемыми параметрами плазмы газового разряда являются сорт плазмообразующего газа, его давление и расход газа , ток разряда (в случае ВЧ и СВЧ разрядов-удельная мощность), а также геометрия плазмохимического реактора и материал, из которого он изготовлен. Стационарное состояние плазмы характеризуется внутреннми параметрами, такими как приведенная напряженность электрического поля E/N, химический состав, включая распределения частиц по различным степеням свободы, и т.д. Величина E/N и другие внутренние параметры устанавливается на таком уровне, чтобы обеспечивался баланс зарядов – скорость их образования равнялась скорости гибели. Низкотемпературная плазма (НТП) является самосогласованной системой – ее физическое состояние, определяющее химическую активность, зависит от скоростей химических реакций. Схема конверсии энергии в НТП приведена на рис.1.

Рис.1 Схема распределения энергии в НТП.
Энергию от внешнего электромагнитного поля приобретают в основном электроны, которые в столкновениях с молекулами плазмообразующего газа, передают ее на различные степени свободы. Химические реакции, протекающие между частицами как в объеме плазмы, так и на ее поверхности, приводят к тому, что состав газа может сильно отличаться от исходного. Все процессы, указанные односторонними стрелками на рис.1, на самом деле взаимосвязаны. Например, электроны не только отдают энергию, но могут и приобретать ее в сверхупругих столкновениях; стенка реактора может быть не только местом, где происходит выделение энергии, взятой от поля, но и дополнительной энергии, если стенка является химически реагирующей. Изменение состава плазмы приводит к изменению характеристик взаимодействия электронов с тяжелыми частицами и, как следствие, изменению характера приобретения энергии от поля и т.д.
Конечно, сложность (уровень) модели, помимо чисто математических сложностей, зависит от конкретных задач, а также определяется объемом фактических сведений, необходимых для расчетов. Если рассматривать НТП разряда постоянного тока, то в качестве модели высшего уровня следует рассматривать такую задачу, в которой задаваемыми параметрами являются только внешние: давление газа, ток разряда и геометрия реактора. Несмотря на сложность, для ряда плазмообразующих газов, таких как азот, водород, кислород, аргон, терафторметан и некоторые других, экспериментальный материал позволяет построить такие модели. Они являются полуэмпирическими в том смысле, что для их реализации необходимы данные о кинетических характеристиках элементарных процессов, хотя можно представить себе и модели более высокого уровня, где эти характеристики определяются соответствующими квантово-механическими расчетами ab initio.
Опыт моделирования плазмы молекулярных газов показывает, что всю сложную модель целесообразно представить в виде следующих подмоделей: 1) кинетики электронного газа 2) колебательной кинетики основных электронных состояний 3) кинетики образования и гибели заряженных частиц 4) кинетики реакций нейтральных частиц 5) тепловых источников 6) электродинамики. Это разделение основано на общности физико-химических процессов, протекающих в каждой подмодели и, как следствие, на общности уравнений, их описывающих.
Конечно, все подмодели являются взаимосвязанными и в общем случае должны рассматриваться совместно. Установление взаимосвязей, степени их тесноты является одной из задач моделирования, поскольку позволяет часто упростить описание всей системы в целом. Один из путей – анализ каждой подмодели, при этом величины, являющиеся решениями другой подмодели, задаются параметрически. Диапазон их изменений берется либо из опыта, либо на основе тех или иных реалистичных оценок. Как показывает опыт, удачное моделирование отдельной подсистемы (получение согласия с опытом) определенным подбором параметров (в том числе и кинетических) не всегда гарантирует правильность. Но если рассматривать сразу несколько подмоделей, то величины, определенные неверно, проявятся в виде результатов, противоречаших эксперименту. Надежность любой модели имеет относительный характер в том смысле, что она верна настолько, насколько не противоречит имеющимся опытным данным. Вероятностной в модели является та информация, которую нельзя проверить к настоящему моменту времени. Эта информация и является источником развития модели. Далее мы рассмотрим возможности и способы моделирования кинетики электронного газа , колебательной кинетики основных электронных состояний и кинетики образования и гибели заряженных частиц, которые наиболее сложны в математическом плане.
II. КИНЕТИКА ЭЛЕКТРОННОГО ГАЗА
Эта подсистема является наиболее важной, так как именно она определяет возможности ? перекачки? энергии внешнего электрического поля в химические реакции. Эта подсистема определяет функцию распределения электронов по энергиям (ФРЭЭ). ФРЭЭ является решением кинетического уравнения Больцмана, которое в двучленном приближении имеет вид
 , (1)
, (1)
где  ; E/N - приведенная
напряженность электрического поля;
e - текущая
энергия электронов; Yk - мольная доля
k-го компонента
смеси; Qktr
- транспортное
сечение взаимодействия электрона с
k-тым
компонентом, а Jу, Jну, Jee - интегралы
упругих, неупругих и
электрон-электронных (e-e)
столкновений.
; E/N - приведенная
напряженность электрического поля;
e - текущая
энергия электронов; Yk - мольная доля
k-го компонента
смеси; Qktr
- транспортное
сечение взаимодействия электрона с
k-тым
компонентом, а Jу, Jну, Jee - интегралы
упругих, неупругих и
электрон-электронных (e-e)
столкновений.
 ,
,
где ![]() - температура
газа, а
- температура
газа, а 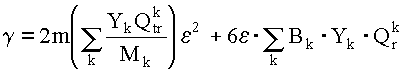 , где
m - масса
электрона; Mk, Bk,
Qkr - масса
молекулы, вращательная постоянная
и сечение возбуждения вращательных
уровней k-го
компонента.
, где
m - масса
электрона; Mk, Bk,
Qkr - масса
молекулы, вращательная постоянная
и сечение возбуждения вращательных
уровней k-го
компонента.
Член, учитывающий возбуждение вращательных уровней, записан вместе с членом, учитывающим упругие соударения, поскольку и те и другие приводят к малым потерям энергии электронами и могут быть учтены в диффузионном приближении.
Интеграл неупругих столкновений Jну - складывается из двух интегралов - J1ну и J2ну, которые описывают соударения 1-го и 2-го рода соответственно:
 ,
,
где суммирование ведется по всем j-тым реакциям для k-го компонента; e jk - пороговая энергия j-той реакции; Qkj - сечение реакции для соударения 1-го рода; а Qk-j - второго рода. Сечения Qkj и Qk-j связаны между собой принципом детального равновесия:
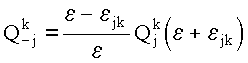 .
.
Интеграл e-e соударений определяется как
 ,
,
где частота e-e соударений n ee и кулоновский логарифм lnl равны
 .
.
В этих
выражениях Ye, ne,
u , e, ![]() - мольная
доля, концентрация, скорость, заряд
и средняя энергия электронов. ФРЭЭ
нормирована в соответствии с
- мольная
доля, концентрация, скорость, заряд
и средняя энергия электронов. ФРЭЭ
нормирована в соответствии с  .
.
Существует много методов решения этого уравнения. Наиболее простой – следующий. Выберем равномерную сетку по энергии с узлами 1, 2 ... m, m+1...N и проинтегрируем уравнение (1) по одному интервалу сетки, то есть от e m до e m+1, вычисляя интегралы неупругих соударений по правилу прямоугольных трапеций. В результате получается система разностных уравнений вида
![]() . (2)
. (2)
Коэффициенты am, bm, cm и dm этой системы равны:
 ,
,
 ,
,
 ,
,
 .
.
В этих выражениях индексы m, m+1, m+1± nj, m± nj указывают на номер узла сетки, в котором определяется соответствующая величина, причем
D e =e m+1-e m, а nj=(e ij-e 1)/ D e + 1 .
Система (2) замыкается двумя граничными условиями, означающими отсутствие потока электронов в пространстве энергий при e =e 1 и e =e N
![]() , (3)
, (3)
![]() . (4)
. (4)
Разностная система уравнений (2)-(4) является консервативной, т.е. удовлетворяет условию сохранения числа электронов в пространстве энергий, если положить, что все значения Qkj, Qk-j равны нулю, для e >e N.
Из-за наличия e-e соударений система уравнений является нелинейной, а члены с неупругими процессами делают ее матрицу разреженной, из-за чего решение с использованием стандартных библиотечных процедур требует большого объема оперативной памяти, что нерационально. Поэтому, удобно применять алгоритм последовательных приближений в сочетании с устойчивым методом прогонки, который заключается в следующем. Берется функция нулевого приближения (можно использовать максвелловскую ФРЭЭ со средней энергией 1 эВ) и с ней вычислить коэффициенты a, b, c и d. Эта процедура сводит матрицу системы к трехдиагональному виду и система быстро решается прогонкой, в результате которой определяется ФРЭЭ следующего приближения и так далее до тех пор, пока не удовлетворяется заданная относительная погрешность. Правильность расчета можно контролировать по выполнению баланса энергий электронов, т.е. при верном решении скорость приобретения энергии электронами от электрического поля должна равняться скорости потерь энергии на все процессы.
На основе
вычисленной ФРЭЭ определяются
такие характеристики электронов
как средняя энергия ![]() , приведенный
коэффициент диффузии DN, скорость
дрейфа VD, константы
скоростей реакций Kkj:
, приведенный
коэффициент диффузии DN, скорость
дрейфа VD, константы
скоростей реакций Kkj:
 ,
,
 ,
,
 ,
,
 .
.
Для анализа этой подсистемы необходимо иметь данные о составе плазмы, величинах E/N, а также о сечениях процессов столкновений электронов с компонентами плазмы. Поскольку порядок сечений взаимодействия электронов с разными молекулами одинаков, то компоненты плазмы, мольная доля которых меньше 10-2 можно не принимать во внимание.
Наиболее доступно методы решения уравнения Больцмана в двучленном приближении изложены в книге [1]. Данные по сечениям взаимодействия электронов с различными молекулами к сожалению разбросаны по многим оригинальным статьям и обзорам. Для N2 и СО2 они приведены в [2], для кислорода в [3], для ряда других используемых в конкретных приложениях газов в обзоре [4].
II. КОЛЕБАТЕЛЬНАЯ КИНЕТИКА
В НТП пониженного давления в наибольшей степени заселены колебательные уровни основных электронных состояний плазмообразующих газов и именно они могут существенно влиять как на химические реакции, так и на формирование ФРЭЭ. Особенностью этой подсистемы является то, что нижние колебательные уровни заселяются преимущественно электронным ударом из основного состояния (e-V-процессы), а далее эта энергия перераспределяется по колебательным уровням за счет обмена колебательными квантами при столкновениях колебательно-возбужденных молекул (КВМ) (V-V обмен) и переходит в тепловую при столкновении невозбужденной молекулы с возбужденной (V-T обмен). Наибольшими вероятностями обладают V-V и V-T процессы, протеакющие с потерей или приобретением одного колебательного кванта. В качестве примера приведем выражение для скорости изменения концентрации на V-том колебательном уровне для плазмы кислорода, в которой, помимо молекул в основном состоянии присутствуют и атомы О(3Р), принимающие участие в процессе V-T релаксации.
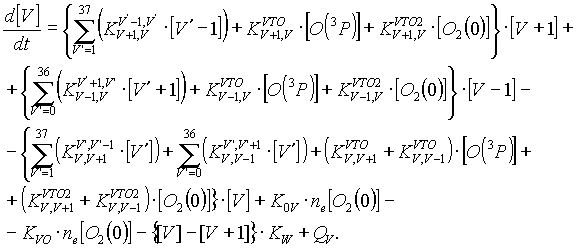 (5)
(5)
В этих
уравнениях: ![]() -
константы скоростей V-T процессов
при соударении атома O(3P) и молекулы O2 на нулевом
колебательном уровне (V=0) с
молекулой на уровне V, при котором
она переходит на уровень V+1;
-
константы скоростей V-T процессов
при соударении атома O(3P) и молекулы O2 на нулевом
колебательном уровне (V=0) с
молекулой на уровне V, при котором
она переходит на уровень V+1; ![]() - константа
скорости V-V процесса, описывающая
обмен колебательными квантами при
столкновении двух молекул на
уровнях с колебательными
квантовыми числами V+1 и V? -1 с переводом
их в состояния V и V? ; K0V и KV0 - константы
скоростей возбуждения и
девозбуждения уровня V электронным
ударом соответственно; KW - эффективная
константа скорости дезактивации в
гетерогенном процессе; QV - член,
описывающий дополнительные
источники образования - гибели
соответствующего состояния;
суммирование ведется по всем
колебательным уровням (V=37 - предел
диссоциации O2(X3S-g) ). Квадратные
скобки символизируют концентрацию
соответствующих компонентов.
- константа
скорости V-V процесса, описывающая
обмен колебательными квантами при
столкновении двух молекул на
уровнях с колебательными
квантовыми числами V+1 и V? -1 с переводом
их в состояния V и V? ; K0V и KV0 - константы
скоростей возбуждения и
девозбуждения уровня V электронным
ударом соответственно; KW - эффективная
константа скорости дезактивации в
гетерогенном процессе; QV - член,
описывающий дополнительные
источники образования - гибели
соответствующего состояния;
суммирование ведется по всем
колебательным уровням (V=37 - предел
диссоциации O2(X3S-g) ). Квадратные
скобки символизируют концентрацию
соответствующих компонентов.
Константы K0V и KV0 должны определяться из ФРЭЭ, а константы скоростей V-T и V-V процессов можно рассчитывать по методике Славского-Шварца-Герцфельда (SSH) с учетом влияния ангармонизма на величину адиабатического фактора и предэкпоненциального множителя :
 , (6)
, (6)
![]() . (7)
. (7)
Если  .
.
Если  .
.
 ,
,![]() при D E<0. (8)
при D E<0. (8)
При D E>0 константа,
вычисленная по (7), домножается
на  .
.
![]() , (9)
, (9)
 , (10)
, (10)
![]() , при Y<20.
(11)
, при Y<20.
(11)
 , при Y>20.
(12)
, при Y>20.
(12)
В
приведенных выражениях М -
приведенная масса партнеров по
соударению в а.е.м., Т - температура
газа в К, w -
колебательный квант в см-1, х -
постоянная ангармонизма в долях
колебательного кванта, a - параметр
крутизны потенциала
взаимодействия в А-1![]() , а константы
, а константы ![]() берутся из
опыта. Константы скоростей прямых и
обратных процессов связаны
принципом детального равновесия.
берутся из
опыта. Константы скоростей прямых и
обратных процессов связаны
принципом детального равновесия.
Для стационарных условий можно рекомендовать проводить решение системы (5) следующим практически опробованным способом. Запишем (5) в виде
![]()
![]() , , (13)
, , (13)
где
коэффициенты аm, bm, cm
и dm сами зависят
от концентраций. По своей структуре
(13) описывает потоки частиц в
пространстве колебательных
уровней. Количество уравнений (13) на
2 меньше, чем число колебательных
уровней. Можно положить, что [37]=0,
выписать отдельно уравнение типа
(13) для нулевого уровня, которое, в
отличие от (13), будет
двухточечным и потребовать, чтобы  . Тогда
скорость частиц, попадающих на 37
уровень, при заданной суммарной
концентрации КВМ и скорости их
накачки, соответствует скорости
диссоциации через колебательный
континуум. Система (13) имеет
диагональное преобладание, поэтому
устойчиво решается методом
прогонки. В нулевой
итерации задается распределение
КВМ по уровням (можно
Больцмановское с реалистической
колебательной температурой),
значение суммарной концентрации
приравнивается величине
концентрации на нулевом уровне,
рассчитываются константы
скоростей и коэффициенты аm,
bm, cm и dm и с ними
решается (13). Решение
перенормируется на суммарную
концентрацию и находится новое
рапределение КВМ и так до
сходимости. Такая процедура легко
модифицируется при наличии двух и
более молекулярных компонентов, а
также других процессов с участием
КВМ. По крайней мере она была
практически использована для смеси
газов N2, O2 ,NO, N и О(3Р).
. Тогда
скорость частиц, попадающих на 37
уровень, при заданной суммарной
концентрации КВМ и скорости их
накачки, соответствует скорости
диссоциации через колебательный
континуум. Система (13) имеет
диагональное преобладание, поэтому
устойчиво решается методом
прогонки. В нулевой
итерации задается распределение
КВМ по уровням (можно
Больцмановское с реалистической
колебательной температурой),
значение суммарной концентрации
приравнивается величине
концентрации на нулевом уровне,
рассчитываются константы
скоростей и коэффициенты аm,
bm, cm и dm и с ними
решается (13). Решение
перенормируется на суммарную
концентрацию и находится новое
рапределение КВМ и так до
сходимости. Такая процедура легко
модифицируется при наличии двух и
более молекулярных компонентов, а
также других процессов с участием
КВМ. По крайней мере она была
практически использована для смеси
газов N2, O2 ,NO, N и О(3Р).
Отметим, что входными параметрами этой подсистемы, помимо уже отмеченных кинетических характеристик, являются также концентрации и температура газа.
В качестве монографий, из которых можно почерпнуть теорию рассмотренных явлений и многие кинетические данные, следует отметить [5,6]. В обзорных работах [7,8] содержатся также данные о константах скоростей.
III. КИНЕТИКА ОБРАЗОВАНИЯ И ГИБЕЛИ ЗАРЯЖЕННЫХ ЧАСТИЦ
Роль этой подсистемы определяется тем, что именно она определяет значения приведенной напряженности электрического поля E/N как функцию суммарной концентрации частиц N, при которых возможно стационарное существование плазмы. Для моделирования этой подсистемы необходимо иметь сведения о механизме ионизации, т.е. иметь набор основных реакций образования и гибели заряженных частиц. Простейшая модель – это диффузионная модель положительного столба Шоттки, в которой предполагается, что положительные ионы и электроны образуются в результате однократной ионизации частиц газа, и гибнут в результате совместной (амбиполярной) диффузии на стенках реактора. Связь между величинами E/N и N в неявной форме для реактора цилиндрической геометрии дается соотношением:
 , (14)
, (14)
где ![]() -константа
скорости ионизации,
-константа
скорости ионизации, ![]() -характеристическая энергия
электронов и приведенная
подвижность полодительных ионов, R- радиус
реактора. Величины
-характеристическая энергия
электронов и приведенная
подвижность полодительных ионов, R- радиус
реактора. Величины ![]() через ФРЭЭ
есть функции E/N для заданного
состава плазмообразующего газа.
через ФРЭЭ
есть функции E/N для заданного
состава плазмообразующего газа.
Подход для анализа этой подсистемы в других более сложных случаях рассмотрим на примере НТП кислорода, механизм ионизации которой может быть описан как следующий.
О2(Х)+е® О2++2е О2(D )+е® О2++2е О(3Р)+е® О++2е О2(Х)+О+® О2++О
О2(Х)+е® О-+О О2(D )+е® О-+О О2(D )+О-® О3+е О-+О® О2+е
О-+О2+® О+О+О
Основными заряженными частицами являются электроны и ионы O+2, O-. Плотности потоков Ге, Г+, Г- этих частиц равны
Ге= - DeN ne -m eneEr Г+= - D+N n+ -m +n+Er Г-= - D-N n- -m -n-Er , (15)
где De, D+, D- - коэффициенты диффузии; m e, m +, m - - подвижности; ne, n+, n- - концентрации электронов, ионов O+2, O- соответственно, а Er - напряженность поля объемного заряда.
В стационарных условиях
Гe+Г-=Гр . (16)
Использовав (15,16) и введя обозначение a =n-/ne, определим величину Er , которая при подстановке в (15)) дает:
 (17)
(17)
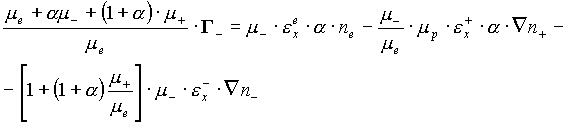 (18)
(18)
 (19)
(19)
Здесь ![]() -
характеристические энергии
электронов и соответствующего
сорта ионов.
-
характеристические энергии
электронов и соответствующего
сорта ионов.
В НТП
обычно реализуется ситуация, когда ![]() , а отношения m е/m +-»
100
, а отношения m е/m +-»
100
Член  сильно
отличается от единицы, если
сильно
отличается от единицы, если  .
.
Эксперимент показывает , что величина a во всяком случае меньше 10. Поэтому этот член можно считать равным 1. Отметим, что такая ситуация реализуется по-видимому и в некоторых других электроотрицательных газах типа СО и СО2, но в галогенсодержащих газах типа Cl2, CF4 величина a может быть и больше 100.
Основываясь на этих же цифрах, можно оценить и члены, содержащие градиенты концентрации. Такие оценки приводят к следующим выражениям для плотностей потоков:
 , (20)
, (20)
![]() , (21)
, (21)
![]() . (22)
. (22)
Поскольку концентрации зарядов связаны между собой условием квазинейтральности плазмы ne+n-=n+, то из трех уравнений непрерывности для Гe, Г- , Г+ можно рассматривать два, а третье будет являться следствием двух других. В цилиндрических координатах для положительных и отрицательных ионов эти уравнения имеют вид
 , (23)
, (23)
 , (23)
, (23)
где Zi, ZПР, ZАО - частоты ионизации, диссоциативного прилипания, ассоциативного отрыва соответственно; Kii и KO - константы скоростей реакций ион-ионной рекомбинации и обдирки электронным ударом. Эти уравнения сводятся к следующему безразмерному виду
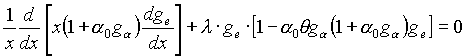 , (24)
, (24)
 (25)
(25)
где x=r/R, R -
радиус реактора; ge=ne/ne0;
ne0=ne при r=0; a 0=a при r=0; ga =a /a 0;
l =Z1.(NR)2/(m +![]() ), Z1=K1Y1+K2Y2+K3Y3,
K1-K3 константы
скорости ионизации O2(X3Sg-), O2(a1Dg), O(3P) электронным
ударом; Y1-Y3 - мольные доли
вышеупомянутых компонентов, N -
суммарная концентрация частиц; P=(Z2m +)/(Z1m -), Z2=K4Y1+K5Y2,
K4-K5 - константы
скорости диссоциативного
прилипания электрона к молекулам O2(X3Sg-) и O2(a1Dg); Q=(Z3m +)/(Z1m -), Z3=K6Y2+K7Y3,
K6-K7 -константы
скорости ассоциативного отрыва
электрона молекулами O2(a1Dg) и атомами O(3P);
q =(K9.Ye0)/Z1,
K9 - константа
скорости ион-ионной рекомбинации; Ye0
-
мольная доля электронов при r=0; j =m +/m -;
W=(K8.Ye0)/Z1 , K8 - константа
скорости обдирки (отрыва) электрона
от иона O- электронным
ударом.
), Z1=K1Y1+K2Y2+K3Y3,
K1-K3 константы
скорости ионизации O2(X3Sg-), O2(a1Dg), O(3P) электронным
ударом; Y1-Y3 - мольные доли
вышеупомянутых компонентов, N -
суммарная концентрация частиц; P=(Z2m +)/(Z1m -), Z2=K4Y1+K5Y2,
K4-K5 - константы
скорости диссоциативного
прилипания электрона к молекулам O2(X3Sg-) и O2(a1Dg); Q=(Z3m +)/(Z1m -), Z3=K6Y2+K7Y3,
K6-K7 -константы
скорости ассоциативного отрыва
электрона молекулами O2(a1Dg) и атомами O(3P);
q =(K9.Ye0)/Z1,
K9 - константа
скорости ион-ионной рекомбинации; Ye0
-
мольная доля электронов при r=0; j =m +/m -;
W=(K8.Ye0)/Z1 , K8 - константа
скорости обдирки (отрыва) электрона
от иона O- электронным
ударом.
Уравнения (24)-(25) дополняются граничными условиями
![]() , (26)
, (26)
 при x=0 ,
(27)
при x=0 ,
(27)
Условия (26)-(27) являются следствием определения величин ga и ge и симметрии задачи. Условия (28) означают, и это можно показать, что отрицательные ионы "заперты" в объеме полем Er , т.е. их плотность потока на стенку реактора Г-(1)=0, а Гe(1)=Г+(1).
Совокупность уравнений (24)-(28) формулирует задачу на собственные значения, т.е. система должна иметь две собственные функции ge и ga и соответствующие им два собственных параметра, в качестве которых были выбраны a 0 и l . Отметим, что l =5.76 в диффузионной теории плазмы не содержащей отрицательных ионов для цилиндрической геометрии (квадрат первого нуля функции Бесселя 1-го рода нулевого порядка). Значение a 0 можно определить, находя ge" из (24) и (25), приравнивая их и используя граничные условия (26) и (27), что дает
 .
(29)
.
(29)
Поскольку все величины, формирующие коэффициенты перед степенями a 0 и величина P, являются положительными, то согласно правилу знаков Декарта алгебраическое уравнение (29) имеет один положительный корень, который, естественно, и обладает физическим смыслом в силу определения величины a 0.
Второе собственное значение l задается выполнением условий (28). Несмотря на то, что с точки зрения математики только два параметра a 0 и l являются собственными значениями, а другие можно задавать произвольно, физически они являются зависимыми.
При заданных мольных долях компонентов, токе разряда i , геометрии реактора R и величине E/N эти величины однозначно определяются видом ФРЭЭ.
Отметим, что входными данными этой подсистемы являются мольные доли компонентов плазмы, подвижности ионов, константы скоростей процессов и, следовательно, величина E/N. Выходные данные – пространственные распределения концентраций заряженных частиц и величины с ними связанные (например, потоки ионов на стенку), а также N- суммарная концентрация частиц, при которой реализуется стационарное состояние НТП.
Полезные экспериментальные данные о транспортных характеристиках различных ионов и способах их оценки можно найти в монографии [9]
ЛИТЕРАТУРА
[ О Школе|Лекции|Секция 1|Секция 2|Секция 3|Секция 4|Секция 5|Cодержание |