УДК 658
ОПТИМИЗАЦИЯ СТРУКТУРЫ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
С.П. Бобков, Н.М. Урюпина
Ивановский государственный химико-технологический университет
А.И.Иванников
ЗАО «НПО «Консультант» г. Иваново
Рассмотрена возможность определения оптимального числа каналов в системе массового обслуживания с использованием экономических критериев. Проведена проверка адекватности модели на данных реального предприятия.
При решении многих экономических задач используется теория систем массового обслуживания (СМО). Опираясь на теорию вероятностей и математическую статистику, эта область прикладной математики занимается анализом процессов в производстве, обслуживании, управлении, т.е. там, где однородные события повторяются многократно или происходит удовлетворение требований на выполнение каких-либо услуг [1]. При этом часто встает вопрос о нахождении оптимального, с точки зрения экономической эффективности, числа каналов СМО. В процессе постановки задачи нами были рассмотрены экономические показатели СМО, которые по своей базовой принадлежности можно разделить на две группы: первая связана с издержками обращения системы, а вторая определяется издержками обслуживания заявок, поступающих на обслуживание [2].
Издержки обращения системы определяются числом занятых каналов, затратами на содержание СМО, интенсивностью обслуживания, степенью загрузки каналов, эффективностью их использования, пропускной способностью СМО и др. Издержки обслуживания заявок, связаны с такими показателями как длина очереди, время ожидания обслуживания, вероятность отказа в обслуживании, время пребывания заявки в СМО и др.
Эти группы показателей противоречивы в том смысле, что улучшение показателей одной группы, например сокращение длины очереди или времени ожидания в очереди путем увеличения числа каналов обслуживания, связано с ухудшением показателей другой группы, поскольку это может привести к увеличению времени простоев каналов обслуживания, затрат на их содержание и т.д. В связи с этим при формализации задач обслуживания вполне естественно стремление построить СМО таким образом, чтобы установить разумный компромисс между показателями, связанными с собственно заявками и полнотой использования возможностей системы. С этой целью необходимо выбрать показатель эффективности СМО, включающий одновременно претензии и возможности обеих групп. В качестве такого показателя был выбран минимум общих затрат [3].
Можно отметить, что в качестве критерия экономической эффективности в целевой функции могут быть так же товарооборот, доход, прибыль, тогда оптимальное значение управляемых показателей СМО находится, очевидно, уже при максимизации указанных показателей.
Рассмотрим СМО с числом каналов n, на вход которой поступает Пуассоновский поток заявок с интенсивностью l. Длительности обслуживания отдельных требований предполагаем случайными с экспоненциальным законом распределения и интенсивностью обслуживания m. Максимально возможное число мест в очереди ограничим величиной m.
Система может иметь следующие дискретные состояния:
S0 – все каналы свободны;
S1 – занят один канал (любой);
- - - - - - - - - - - - - - - - - - - - - -
Sn –заняты все n каналов;
Sn+1 –заняты все n каналов и одна заявка стоит в очереди;
- - - - - - - - - - - - - - - - - - - - - -
Sn+m –заняты все n каналов и все m мест в очереди.
Граф состояний n-канальной СМО с очередью, ограниченной m местами, представлен на рисунке

Рис. Граф состояний n-канальной СМО с очередью длиной m
В узлах графа указаны состояния системы, дуги графа размечены плотностями вероятностей переходов.
На основании представленного графа можно составить алгебраическую систему уравнений для определения вероятностей pi состояний системы в установившемся режиме [4].
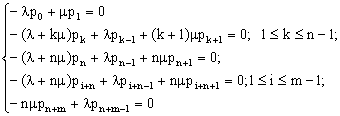 (1)
(1)
Условие нормировки вероятностей имеет вид:
![]() (2)
(2)
Решая систему уравнений, можно определить искомые вероятности, которые, в свою очередь, позволяют вычислить интересующие нас характеристики системы.
Средняя длина очереди определяется из условия, что очередь возникает, когда заняты все каналы и количество заявок в системе варьирует от n+1 до n+m. Поэтому:
![]() (3)
(3)
Отказ в обслуживании происходит, когда заняты все каналы и все места в очереди ожидания. Следовательно, вероятность отказа pОТК = pn+m.
Вероятность потерь из-за отказа в обслуживании уменьшается с увеличением длины очереди и особенно сильно с увеличением числа обслуживающих приборов. Наличие очереди в системе позволяет снизить потери из-за отказа в обслуживании, но вызывает необходимость ожидания заявки в очереди перед началом обслуживания.
Среднее число занятых и свободных (простаивающих) каналов будет, соответственно, равно:
![]() (4);
(4);
![]() (5)
(5)
Рассмотрим основные экономические показатели функционирования системы.
Издержки, связанные с обращением системы СИС, включающие затраты, связанные с эксплуатацией СМО и простоем каналов обслуживания:
![]() (6),
(6),
где СПР и СЭКС – издержки простоя и эксплуатации одного канала.
Можно заметить, что с увеличением числа обслуживающих каналов СМО издержки обращения системы растут.
Издержки обслуживания заявок включают потери, связанные с пребыванием заявок в очереди и с уходом не обслуженных заявок:
![]() (7),
(7),
где СОЧ – потери из-за простоя заявки в очереди; издержки СОТК – потери, вследствие отказа в обслуживании (упущенная прибыль).
Издержки обслуживания заявок с увеличением числа каналов падают, поскольку сокращается число заявок в очереди и уменьшается вероятность отказа в обслуживании.
Общие издержки, которые в данной постановке задачи выступают в роли целевой функции:
С = (СИС + СИЗ). (8)
Таким образом, математически поставленную задачу можно сформулировать, как минимизацию функции (8). В качестве варьируемого параметра СМО, подлежащего определению, было взято число каналов n при заданных интенсивностях обслуживания и потока заявок.
Рассмотренная задача была реализована с помощью пакета математического моделирования Matlab 6. В качестве объекта исследования было взято предприятие, занятое перевозкой пассажиров маршрутными такси, которое предоставило некоторые экономические показатели. В частности были использованы следующие данные. Интенсивность обслуживания пассажиров одним микроавтобусом - m = 25,3 чел/час. Интенсивность пассажиропотока в «часы пик» - l = 500 чел/час, в иное время l = 85 чел/час. Количество мест в очереди m, т.е. количество человек, которые готовы подождать следующего таксомотора, если им не удалось уехать на предыдущем, было взято равным 2.
В ходе компьютерного эксперемента были получены следующие результаты.
Для случая, когда l=500 чел./час, оптимальное число таксомоторов, рассчитанное по модели, равно 29. Вероятность отказа в обслуживании составит 0,5%, средняя длина очереди – 0,02 чел, средняя загрузка машины – 70%. Для случая, когда l=85 чел./час, оптимальное число таксомоторов, рассчитанное по модели, равно 10. Вероятность отказа в обслуживании составит 1,5%, средняя длина очереди – 0,05 чел, средняя загрузка машины – 66%.
Анализ результатов показывает, что система в полном объеме обслуживает все поступающие в нее требования. Однако, несмотря на минимальные издержки, она в обоих случаях загружена не полностью.
Попытка определить статистические показатели при полной загрузке микроавтобусов показала следующее. Полная загрузка системы при l=500 чел./час возможна в случае использования 19 таксомоторов. Но в этом случае вероятность отказа в обслуживании возрастет до 14%, что вызовет повышение издержек, связанных с пребыванием заявок в очереди и с уходом не обслуженных клиентов. Аналогичная картина наблюдается и при l=85 чел./час, когда полная загрузка системы происходит для n=6. Здесь вероятность отказа составит уже 22%.
В результате проведенного исследования можно сделать выводы:
Применение элементов теории массового обслуживания в сочетании с экономическими критериями может позволить снизить затраты предприятия путем оптимизации структуры производства.
Проверка адекватности предложенной модели на данных реального предприятия показала, что данный подход может быть применен в практике оперативного управления. Результаты работы модели можно считать корректными при достоверных исходных данных.
Литература
1. Рыжиков Ю.И. Теория очередей и управление запасами. – СПб.: Питер, 2001. – 384с.
2. Савицкая Г.В. Анализ хозяйственной деятельности предприятия – М.: ООО “Новое знание”, 2002. – 460с.
3. Фомин Г.П. Математические методы и модели в коммерческой деятельности. – М.: Финансы и статистика, 2001. – 547с.
4. Советов Б.Я., Яковлев С.А. Моделирование систем – М.: Высшая школа, 2001. – 380с.
STRUCTURE OPTIMIZATION OF SERVICE SYSTEM
S. Bobkov, A. Ivannikov, N. Uryupina
The opportunity of definition of optimum number of channels in service system with use of economic criteria is considered. Check of adequacy of model on the data of the real enterprise is executed.